재귀 알고리즘 분석

 

어떠한 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의되는 경우 재귀(recursion)라고 한다. 

 

재귀를 사용하는 대표적인 예로 팩토리얼(factorial) 문제가 있다. 팩토리얼은 양의 정수를 순서대로 곱한다는 의미다. 양의 정수 n의 팩토리얼(n!)은 다음과 같이 재귀적 정의를 할 수 있다.

(재귀 과정으로 팩토리얼값을 구하는 문제는 재귀의 원리를 이해하기 위한 예제일 뿐 알고리즘 문제를 풀 때 현실적으로 적절하지 않다.)

 

def factorial(n :int):
    if n > 0:
        return n * factorial(n - 1)
    else:
        return 1
    
if __name__ == '__main__':
    n = int(input('출력할 팩토리얼 값을 입력하세요 : '))
    print(f'{n}의 팩토리얼은 {factorial(n)}입니다.')

 

factorial() 함수는 n - 1의 팩토리얼값을 구하기 위해 다시 자신과 똑같은 factorial() 함수를 호출한다. 이런 함수의 호출을 재귀 호출(recursive call)이라고 한다.

 

 

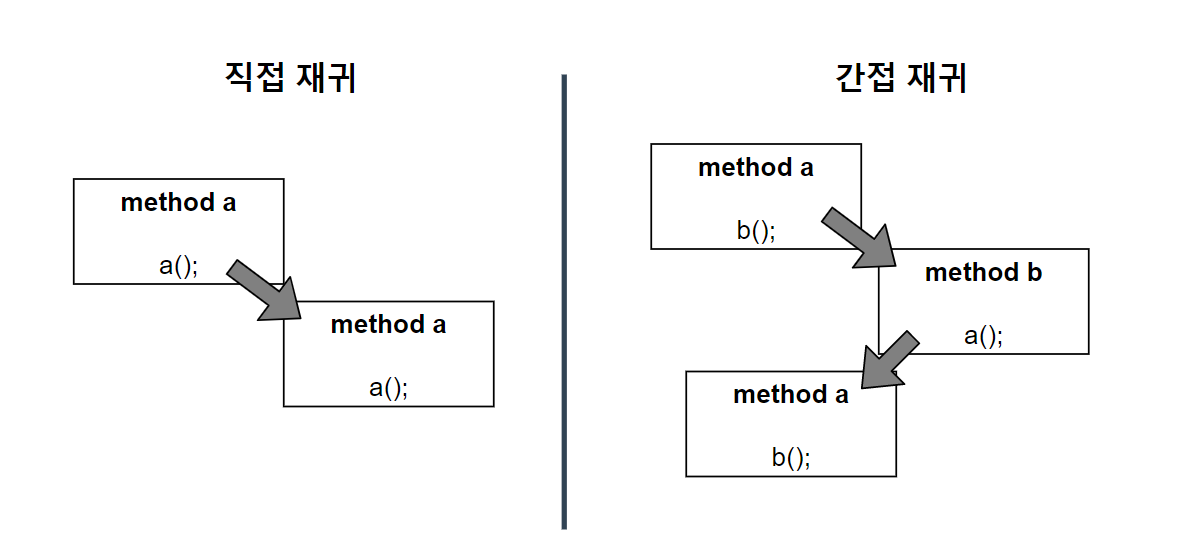
직접 재귀와 간접 재귀

자신과 똑같은 함수를 호출하는 방식을 직접 재귀라고 한다. 간접 재귀는 a() 함수가 b() 함수를 호출하고 다시 b() 함수가 a() 함수를 호출하는 구조다.

 

 

 

유클리드 호제법

22와 8의 최대 공약수를 구하는 과정

 

두 정숫값의 최대 공약수(GCD)를 재귀적으로 구하는 방법이다. 두 정숫값이 주어질 때 큰 값을 작은 값으로 나누어 떨어지면 작은 값이 최대 공약수가 된다. 나누어 떨어지지 않으면 작은 값과 나머지에 대해 같은 과정을 나누어 떨어질 때까지 재귀적으로 반복한다.

이 알고리즘을 유클리드 호재법(Euclidean algorithm)이라고 한다.

 

#-- 유클리드 호재법으로 최대 공약수 구하기

def gcd(x, y):
    if y == 0:
        return x
    else:
        return gcd(y, x % y)
    
if __name__ == '__main__':
    x = int(input('첫 번째 정숫값을 입력하세요 : '))
    y = int(input('첫 번째 정숫값을 입력하세요 : '))
    print(f'두 정숫값의 최대 공약수는 {gcd(x, y)}입니다.')

 

---

 

재귀 알고리즘 분석

아래의 코드는 recur() 라는 재귀 함수와 함수를 호출하는 code로 구성되어 있다. 간단하게 재귀 호출을 여러 번 실행하는 것처럼 보이지만 실제 동작은 복잡하다. 매개변수 n에 4를 전달하면 recur() 함수는 1, 2, 3, 1, 4, 1, ,2를 한 줄에 출력한다.

재귀 호출하는 recur() 함수를 하향식(top-down)과 상향식(bottom-up) 방법으로 분석해보자.

 

def recur(n):
    if n > 0:
        recur(n - 1)
        print(n)
        recur(n - 2)
        
x = int(input('정숫값을 입력하세요 : '))
recur(x)

 

하향식 분석

매개변수 n에 4를 전달하면 다음과 같은 순서로 진행된다.

 

recur(4)의 실행과정 1. recur(3)을 실행 2. 4를 출력 3. recur(2)를 실행

 

위의 과정 2에서 4가 출력되려면 recur(3)의 실행을 완료한 뒤이기 때문에 recur(3)이 먼저 끝나야 한다.

 

각각의 상자는 recur()의 동작을 나타낸다. 전달받은 값이 0 이하이면 -를 표시한다.

 

내용을 정리하면 '왼쪽 화살표를 따라 1칸 아래쪽 상자로 이동하고, 다시 원래 호출한 상자로 되돌아오면 ⬛ 안의 값을 출력한다. 이어서 오른쪽 화살표를 따라 1칸 아래쪽 상자로 이동한다.'를 하나의 단계로 생각해야 한다. 이 단계를 1번 끝내야 1칸 위쪽 상자로 올라갈 수 있다.

 

위의 그림을 보면 recur(1), recur(2)를 여러 번 호출하고 있다. 하향식으로 분석하면 이렇게 같은 함수를 여러 번 호출할 수 있으므로 반드시 효율적이지 않다.

 

 

상향식 분석

상향식 분석은 아래쪽부터 쌓아 올리며 분석하는 방법이다. recur() 함수는 n이 양수일 때만 실행하므로 먼저 recur(1)이 어떻게 처리되는지 알아야 한다.

 

recur(1)의 실행 과정 1. recur(0)을 실행한다. 2. 1을 출력한다. 3. recur(-1)을 실행한다.

 

결국 과정 2의 1만 출력한다는 것을 알 수 있다. recur(2)를 실행하면 과정 1에서 recur(1)은 출력하지만 과정 3의 recur(0)은 아무것도 출력하지 않는다. 결국 recur(1)과 recur(2)의 과정을 거쳐서 1과 2를 출력한다.  이 과정을 통하여 recur(4)의 최종 출력을 얻을 수 있다.

 

 

 

 

 

재귀 알고리즘의 비재귀적 표현

 

꼬리 재귀 제거하기

recur() 함수의 맨 끝에서 재귀 호출하는 꼬리 재귀 recur(n -2) 함수의 의미는 '인수로 n - 2의 값을 전달하고 recur() 함수를 호출하는 것'이다. 따라서 'n의 값을 n - 2로 업데이트하고 함수의 시작 지점으로 돌아갑니다.'와 같이 해석할 수 있다. 이 동작을 반영하여 함수를 다음과 같이 수정할 수 있다.

 

def recur(n):
    while n > 0:
        recur(n - 1)
        print(n)
        n = n - 2

 

이렇게 하면 recur() 함수의 맨 끝에서 실행된 재귀 호출인 꼬리 재귀(tail recursion)를 쉽게 제거할 수 있다.

 

 

재귀 제거하기

꼬리 재귀와 달리 recur(n - 1) 함수는 제거하기 쉽지 않다. n 값을 촐력하기 전에 recur(n - 1)을 실행해야 하기 때문이다. 예를 들어 n값이 4인 경우 재귀 호출 recur(3)의 처리가 완료될 때까지 4를  임시로 저장해야 한다. 또한 앞의 처리가 끝난다면 다시 값을 꺼내 출력해야 한다. 이러한 문제는 stack으로 해결할 수 있다.